二輪車における前輪の幾何学　フロントタイヤの接地点は、操舵でどうかわる？

アマリングなどを論じた動画に、新たなコメントがありました。

発信者として意図しない受け取られ方があっても、それほど気にしないのですが、理論的な間違いには注意が必要です。

それを正した動画もありますが、今回はブログでもその内容を証明していきます。

１　フロントタイヤは複雑な機構で取り付けられている

２　接地点と回転軸がずれている

３　バンクと操舵

４　まとめ

１　フロントタイヤを保持する機構の解説

フロントタイヤは複雑な要素を持つ機構により、保持（取付）されています。

a　キャスター角
b　フロントフォークオフセット

この二つが操舵（ハンドルを切る行為）による動きを複雑にしています。

a まずキャスター角ですが、フロントフォークは垂直ではなく、概ね24～27°程度傾いて取り付けられています。

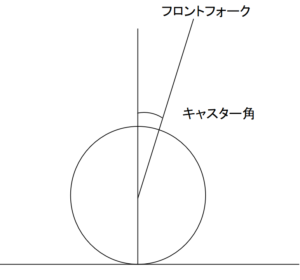
b 次にフォークオフセットですが、これはフロントフォークの取り付け軸と、ハンドル系の回転軸の位相（ずれ）の事です。これがフロント周りにトレールを生み出します。

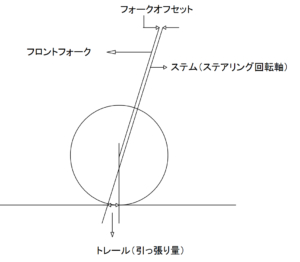
オフロードバイクではフロントフォークの前輪保持を前方に突き出すことで、さらにトレール量を調整しています。

２　接地点と回転軸がずれている

bの図を見てください。フロントフォークの軸と、ステアリングの軸がずれています。これにより操舵による「前輪の回転軸」は「ステムの回転軸」よりも後方にあることが理解（証明）できました。

３　バンクと操舵

バンク角が増えればタイヤの接地点が外側へ移動するのは明確です。それでは操舵がタイヤ接地点にはどのように影響するのか、思考実験を通して明らかにしましょう。

以下をあらかじめ定義しておきます。
・接地点は変形のないものと仮定します。
・接地点は点接触とします。

c　仮にフロントフォークが直立（キャスター角0°）し、フォークとステムの両軸が同一ならば、フロントタイヤの接地面は操舵により変化しません。これはバンク角も関係しません。

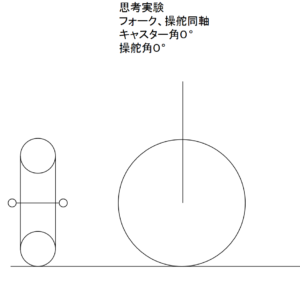
d　フロントフォークが90°倒れていると仮定します。ここでもフォークとステムの両軸は同一とします。

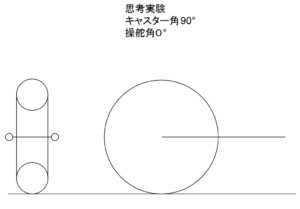
e フォークのキャスタ角が90°の場合は操舵により、接地面が外側へ移動するのがわかります。バンク角が０度でも接地点は外側へ移動することが証明できました。

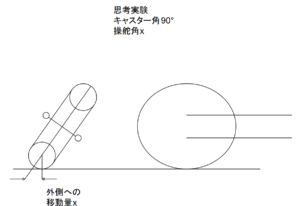
f　次に上記の内容をまとめつつ、数式で証明します。キャスター角を0度とします。

x=r⋅sin(δ)⋅cos(θ)

y=r⋅sin(δ)⋅sin(θ)

z=r⋅cos(δ)

• 横方向の移動 (x方向)：x=r⋅sin(δ)⋅cos(θ)
  • 問題点: この式は、操舵角 $\delta$ がある際に、キャスター角 $\theta$ の影響を受けて接地点が横方向に移動することを示しています。キャスター角が大きくなるにつれて、接地点は外側に移動することを表しています。この点は正しい。
• 縦方向の移動 (y方向)：y=r⋅sin(δ)⋅sin(θ)
  • 問題点: この式は、接地点の縦方向への移動を示します。キャスター角 $\theta$ により、操舵角 $\delta$ の影響で接地点が前後に移動することを表しています。縦方向の移動としては適切です。
• z方向の移動（接地点の高さ）：z=r⋅cos(δ)
  • 問題点: これは接地点の高さ（z方向の位置）を示していますが、キャスター角の影響を含んでいないため、操舵時のz軸の挙動を十分に反映していません。特にキャスター角が加わると、操舵角 $\delta$ により z軸上の変化も生じるため、この式は正確ではありません。

g　ここではキャスター角が24度と仮定し、数式で証明します。

x=r⋅sin(δ)⋅cos(24∘)

y=r⋅sin(δ)⋅sin(24∘)

z=r⋅cos(δ)

1. x方向の移動：x=r⋅sin(δ)⋅cos(24∘)
   この式は、操舵角 $\delta$ に基づき、キャスター角 24° による接地点の横方向への移動を示しています。キャスター角があるため、前輪が左右に動く際に接地点は外側にずれます。これは適切です。
2. y方向の移動：y=r⋅sin(δ)⋅sin(24∘)
   この式は、キャスター角 24° による縦方向の移動を表しています。操舵角 $\delta$ に応じて、接地点が前後にずれることを示しています。これも正しい式です。
3. z方向の移動：z=r⋅cos(δ)
   この式は、接地点の高さ方向への移動を示しています。操舵角 $\delta$ によって z方向に影響を与えるが、キャスター角を直接考慮していないため、z方向にはキャスター角が影響しないと仮定した場合には正しいと言えます。

結論：

• x方向とy方向の式は、キャスター角 24°を考慮した操舵による接地点の移動を正しく表しています。
• z方向の式も、操舵による接地点の高さ変化を表しており、キャスター角の影響を考慮しない場合には正しいといえます。

４　まとめ

長くなりましたが、これでキャスター角が操舵により、前輪の接地点を外側へ移すことが明らかになりました。

バイクの前輪は複雑な運動をするので、直感的には理解しずらい面があるかもしれませんが、複合的な運動の一つ一つを取り出して、分解すれば意外と容易に得心することも可能です。

参考文献は以下の通りです。
・二輪車の前輪系の幾何学　1) 景山 克三, 2) 傳 啓泰　（国会図書館で確認できます）
・図説　バイク工学入門　和歌山利宏　著
・タイヤの科学とライディングの極意　和歌山利宏　著
・ライダーのための基礎工学　和歌山利宏　著
・サーキットライディングを科学する　和歌山利宏　著
・Chat GPT